作为一个管理者首先要考虑的是在无情的市场竞争中怎么样生存,前面几篇连续讲风险的概念,无非就是帮助管理者有了风险意识后能帮助识别翻船的因素并找到应对的方法。这次跟同学们聊一聊一个全新概念-博弈论,至于为什么说全新,这是你看完这篇文章的感受,如果以前你学习过有了解那一定是我用词不当。
首先还是讲一讲博弈论的定义(概念),当然还是索引自号称自由的百科全书的“维基百科”,有条件(FQ)的同学也可以比对下我COPY的对不对,没条件的同学就将就着看吧。
博弈论(英语:Game Theory),又译为对策论或赛局理论,是经济学的一个分支,1944年冯·诺伊曼与奥斯卡·摩根斯特恩合著《博弈论与经济行为》,标志着现代系统博弈理论的的初步形成,因此他们被称为“博弈论之父”。博弈论被认为是20世纪经济学最伟大的成果之一。目前可以应用在生物学、经济学、国际关系、计算机科学、政治学、军事战略,研究游戏或者博弈内的相互作用。是研究具有斗争或竞争性质现象的数学理论和方法。也是運籌學的一个重要学科。 现代的博弈论的源头是约翰·冯·诺伊曼对于双人零和博弈的混合策略均衡点的发想和证明。
概述:博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。表面上不同的相互作用可能表现出相似的激励结构(incentive structure),所以它们是同一个游戏的特例。其中一个有名有趣的应用例子是囚徒困境。具有竞争或对抗性质的行为称为博弈行为。在这类行为中,参加斗争或竞争的各方各自具有不同的目标或利益。为了达到各自的目标和利益,各方必须考虑对手的各种可能的行动方案,并力图选取对自己最为有利或最为合理的方案。比如日常生活中的下棋,打牌等。博弈论就是研究博弈行为中斗争各方是否存在着最合理的行为方案,以及如何找到这个合理的行为方案的数学理论和方法。生物学家使用博弈理论来理解和预测进化(论)的某些结果。例如,John Maynard Smith和George R. Price在1973年发表于《自然》杂志上的论文中提出的“进化稳定对策”的这个概念就是使用了博弈理论。还可以参见进化博弈理论和行为生态学(behavioral ecology)。博弈论也应用于数学的其他分支,如概率、统计和线性规划等。
博弈分类:博弈的分类根据不同的基准也有不同的分类。一般认为,博弈主要可以分为合作博弈和非合作博弈。它们的区别在于相互发生作用的当事人之间有没有一个具有约束力的协议,如果有,就是合作博弈,如果没有,就是非合作博弈。从行为的时间序列性,博弈论进一步分为两类:静态博弈是指在博弈中,参与人同时选择或虽非同时选择但后行动者并不知道先行动者采取了什么具体行动;动态博弈是指在博弈中,参与人的行动有先后顺序,且后行动者能够观察到先行动者所选择的行动。通俗的理解:“囚徒困境”就是同时决策的,属于静态博弈;而棋牌类游戏等决策或行动有先后次序的,属于动态博弈。按照参与人对其他参与人的了解程度分为完全信息博弈和不完全信息博弈。完全博弈是指在博弈过程中,每一位参与人对其他参与人的特征、策略空间及收益函数有准确的信息。如果参与人对其他参与人的特征、策略空间及收益函数信息了解的不够准确、或者不是对所有参与人的特征、策略空间及收益函数都有准确的准确信息,在这种情况下进行的博弈就是不完全信息博弈。目前经济学家们现在所谈的博弈论一般是指非合作博弈,由于合作博弈论比非合作博弈论复杂,在理论上的成熟度远远不如非合作博弈论。非合作博弈又分为:完全信息静态博弈,完全信息动态博弈,不完全信息静态博弈,不完全信息动态博弈。与上述四种博弈相对应的均衡概念为:纳什均衡、子博弈精炼纳什均衡、贝叶斯纳什均衡、精炼贝叶斯纳什均衡(perfect Bayesian Nash equilibrium)。博弈论还有很多分类,比如:以博弈进行的次数或者持续长短可以分为有限博弈和无限博弈;以表现形式也可以分为一般型(战略型)或者展开型等等。
博弈论相关概念
纳什均衡:在博弈论中,纳什均衡(英语:Nash equilibrium,或称纳什均衡点)是指在包含两个或以上参与者的非合作博弈(Non-cooperative game)中,假设每个参与者都知道其他参与者的均衡策略的情况下,没有参与者可以透过改变自身策略使自身受益时的一个概念解。[1]该术语以约翰·福布斯·纳什命名。在博弈论中,如果每个参与者都选择了自己的策略,并且没有玩家可以透过改变策略而其他参与者保持不变而获益,那么当前的策略选择的集合及其相应的结果构成了纳什均衡。

囚徒困境:是博弈论的非零和博弈中具代表性的例子,反映个人最佳选择并非团体最佳选择。或者说在一个群体中,个人做出理性选择却往往导致集体的非理性。虽然困境本身只属模型性质,但现实中的价格竞争、环境保护等方面,也会频繁出现类似情况。
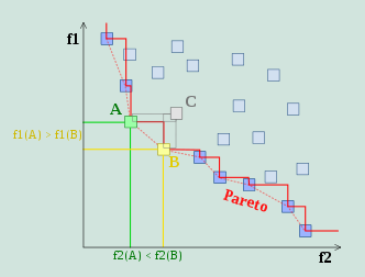
帕累托最优:帕累托最适(英语:Pareto optimality),或称帕累托效率(英语:Pareto efficiency),是经济学中的重要概念,并且在博弈论、工程学和社会科学中有着广泛的应用。与其密切相关的另一个概念是帕累托改善。帕累托最优是以提出这个概念的意大利社会学家维弗雷多·帕累托的名字所命名。帕累托最优是指资源分配的一种理想状态。给定固有的一群人和可分配的资源,如果从一种分配状态到另一种状态的变化中,在没有使任何人情况变坏的前提下,使得至少一个人变得更好,这就是帕累托改善。帕累托最适的状态就是不可能再有更多的帕雷托改善的状态;换句话说,不可能在不使任何其他人受损的情况下再改善某些人的情况。
零和博弈:(英语:zero-sum game),又称零和游戏或零和赛局,与非零和博弈相对,是博弈论的一个概念,属非合作博弈。零和博弈表示所有博弈方的利益之和为零或一个常数,即一方有收入,其他方必有所失。在零和博弈中,博弈各方是不合作的。非零和博弈表示在不同策略组合下各博弈方的得益之和是不确定的变量,故又称之为变和博弈。如果某些战略的选取可以使各方利益之和变大,同时又能使各方的利益得到增加,那么,就可能出现参加方相互合作的局面。因此,非零和博弈中,博弈各方存在合作的可能性。国际经济中许多问题都属于非零和博弈问题,即国际经济中各方的利益并不是必然相互冲突的。零和博弈的例子有赌博、期货和选举等。
非零和博弈与零和博弈相对。非零和博弈表示在不同策略组合下各博弈方的得益之和是不确定的变量,故又称之为变和博弈(variable-sum / non-constant-sum game)。零和博弈表示所有博弈方的利益之和为零或一个常数,即一方有收入,其他方必有所失。在零和博弈中,博弈各方是不合作的。如果某些战略的选取可以使各方利益之和变大,同时又能使各方的利益得到增加,那么,就可能出现参加方相互合作的局面。因此,非零和博弈中,博弈各方存在合作的可能性。国际经济中许多问题都属于非零和博弈问题,即国际经济中各方的利益并不是必然相互冲突的。在这种状况中,自己的收入并不与他人所失之大小相等,而自己的幸福也不一定建立在他人的痛苦之上,即使伤害他人也可能“损人不利己”,所以博弈双方存在双赢的可能,进而合作。
序贯博弈(英语:sequential game),是指在博弈中,一个参与者先于另一个参与者行动。值得注意的是,后者必须至少能获得先发者的部分行为信息,否则行为时间的先后就不会有任何效应。许多棋类游戏都是序贯博弈,如井字棋、象棋、国际象棋、围棋等。决策树的大小可以根据游戏的复杂性而有所不同,范围从一个小而详尽的游戏树的井字棋,而围棋决策树如此之大,甚至电脑无法完全映射出的非常复杂的博弈树。
上面只是列举了部分典型的博弈类型,其实还有很多种类型,看下图:
(本来要贴维基百科的可链接页面,因技术水平有限,字体太大且总是调整不了,无奈搞了个截图,想想即使有链接大部分同学也打不开,就不研究了,想了解更多的同学打开这里 博弈论)

“博弈论”的发展史:要聊这个话题,约翰·冯·诺伊曼(John von Neumann)当然是个无法绕过的人物。

这家伙是个【超级跨界牛人】,即使用这么夸张的称呼,依然不足以体现此人的牛逼之处——他同时在“数学、物理学、经济学、计算机”等多个领域作出了划时代的贡献,并留下一大堆以他命名的东东,比如程序员应该都听说过“冯诺依曼体系”,比如数学领域有“冯诺依曼代数、冯诺依曼遍历定理…”,理论物理领域有“冯诺依曼量子测量、冯诺依曼熵、冯诺依曼方程…”。另外还有很多东东,虽没有以他命名,也是他先搞出来滴,比如:量子力学的公理化表述、希尔伯特第5问题、连续几何(其空间维数不是整数)、蒙特卡洛方法、归并排序算法……
1944年,他与奥斯卡·摩根斯坦(Oskar Morgenstern)合作发表了《博弈论与经济行为》(洋文叫做“Theory of Games and Economic Behavior”),一举奠定博弈论体系的基础,所以他也被称作【博弈论之父】。
这个《博弈论与经济行为》一开始是以论文形式写成,长达1200页,基本上是冯·诺伊曼一个人的手笔。有些同学会纳闷了——那摩根斯坦凭啥当第二作者呀?这里面大致有2个原因:
其一,摩根斯坦本人非常看好“博弈领域的研究”,他认为:该领域的研究可以为一切经济学理论建立正确的基础。当他结识了冯大牛之后,就一直劝说这只大牛写篇该领域的论文。
其二,当冯大牛完成上千页的论文之后,摩根斯坦为这篇论文补了一个非常有煽动性的“绪论”,使得这篇论文一发表就在数学界&经济学界产生轰动效果。
所以,把摩根斯坦列为第二作者,也算说得过去。
另外,这本《博弈论与经济行为》的某些思想源自冯·诺伊曼在1928年发表的论文《On the Theory of Parlor Games》。因此有些学者认为1928年才是真正意义上的博弈论诞生之年。
下面聊聊典型的案例:
(二战中)新几内亚的航路作战:这是一个很经典的博弈论案例,很多博弈论的科普读物都引用了此案例。比如俺分享的那本《纳什均衡与博弈论——纳什博弈论及对自然法则的研究》就包含了这个案例。
话说太平洋战场上,美日双方对新几内亚岛展开争夺战。美方通过截获的情报得知日方有一支补给船队要开往该岛。日军补给船队有两条路线可走(北线 or 南线),两条路线都耗时3天。在南线,这3天都是晴天;在北线有2天是晴天,1天是阴雨(阴雨天会影响美军轰炸)。美方空军将领手头只有一个飞行队,需要决策:把这个飞行队派到哪一边执行轰炸任务?如果押宝的方向错误,重新部署又会浪费掉1天时间。对这个博弈过程,美方的收益矩阵参见下述表格。表格中的数字表示“可用来轰炸的天数”(对美军而言,这个数字越大越好)。

从上述收益矩阵来看,美军应该选哪个策略,不那么明显。但如果【换位思考】,看日军的策略,就非常明显啦。
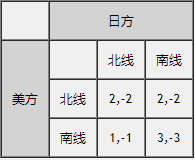
第2个表格补充了日方的收益(以逗号分隔)。由于日方是遭受轰炸,其收益以“负数”表示。从日方的角度(表格的【纵向】角度)来看,走北线是其【支配策略】——不论美方如何选择,日方走北线的收益都不比南线差。对应到刚才介绍的概念,日方的这个“支配策略”属于“弱支配策略”。知道日军必定走北线之后,美军就很容易选定自己的策略了。
静态博弈:假设你是 A(你有三个策略:A1、A2、A3),你的对手是 B(也有三个策略:B1、B2、B3)。 以下是针对 A(你)的收益矩阵:
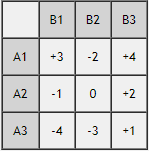
针对上述收益矩阵,基于 Minimax 算法,你应该选择 A2 策略——此时你的最坏情况是 -1。
动态博弈——切蛋糕博弈:当双方都是足够理性,选蛋糕的人肯定会选大的那块。切蛋糕的人基于“最小最大原则”,应该在最坏情况下最小化自己的损失,所以他/她应该把蛋糕切成同等大小。
海盗博弈(海盗分金问题):5个海盗抢了100个金币,讨论如何分赃。这5个海盗有等级高低(不妨假设 A>B>C>D>E)。先由等级最高的海盗提出分赃方案,然后投票。如果半数以上(含半数)同意,就按这个方案分,游戏结束;如果同意的不到半数,把提出方案的海盗扔进海里喂鲨鱼,然后由次一等级的海盗提出新的方案;以此类推。每个海盗的特点是:足够理性(追求个人利益最大化)并且知道别人也足够理性;足够残忍(在个人利益等同的情况下,倾向于把更多同伴扔进海里)。
博弈策略分析:为了进行反向推理,假设最后只剩下2个海盗(D & E)。此时的投票肯定过半(D 肯定投票赞同自己的方案)。在这种局面下,D 可以采用最极端的方案——自己全拿100个金币,E 则一个也拿不到。
现在回推一步。当只剩下3个海盗(C、D、E),由 C 提出方案。他只需要分1个金币给 E,E 就会投票支持(否则的话,等到由 D 来提方案,E 啥也拿不到)。所以在 C 的方案中,他自己拿99个金币,E 拿1个金币。
再往前一步。只剩下4个海盗(B、C、D、E),B 提方案,他当然也能想到刚才那些推理。他只需给 D 1个金币,D 就会支持他(如果等到 C 来提方案,D 啥也拿不到)。所以 B 提出的方案是 B:99,C:0,D:1,E:0,同样能得到半数支持。
基于上述分析,再看 A 的方案,就很显然了——A:98,B:0,C:1,D:0,E:1
有些同学可能会觉得:A 还可以提出另一个等价方案 A:98,B:0,C:0,D:1,E:1(把 C & D 交换)
其实这个方案【不】等价。如果是后面这个方案,D 会投反对票,于是 A 去喂鲨鱼,由 B 来提方案,D 还是可以拿到1个金币。虽然两种方案,D 都是拿1个金币。但基于规则中提到的【残忍性】,D 会对 A 的方案投反对票。
海盗分金的推广:如果你凭直觉认为:总是最先提出方案的海盗占最大利益,那你就犯了直觉谬误啦。
这个博弈游戏还可以推广到更多海盗。当海盗数量达到某个临界点之后,第一个提出方案的海盗必死无疑(必定被丢进海里喂鲨鱼)。
更详细的介绍,可以参见维基百科的“这个链接”。(没条件翻墙的同学不勉强)
囚徒的困境:假设有两个小偷A和B联手闯入民宅盗窃被抓,警方将两人置于不同的房间进行审讯,并给出如下政策:如果一个犯罪嫌疑人坦白并交出了赃物,两人都会被判有罪。如果另一个犯罪嫌疑人也坦白,则两人各被判刑8年;如果另一个犯罪嫌人抵赖,再加刑2年,而坦白者有功,会被立即释放。如果两人都抵赖,偷窃罪证据不足,但会因私入民宅而各判入狱1年。即:

表中的数字表示A,B各自的判刑结果。博弈论分析中一般都用这样的表来表示。此时有人会觉得双方都抵赖就好了,但问题是双方被隔离,都会怀疑对方会出卖自己以求自保。两个人都会这么想:假如对方坦白,此时如果我抵赖得坐10年监狱,如果我坦白才坐8年监狱;假如对方抵赖,此时如果我也抵赖会被判1年,如果我坦白可以被释放。综合以上考虑,不管对方坦白与否,对我而言都是坦白划算。此时最后的“纳什均衡”只能是两个人都坦白,共同被判8年刑期。
智猪博弈:猪圈里有两头猪,一头大猪,一头小猪。猪圈的一边有个踏板,每踩一下踏板,在远离踏板的猪圈的另一边的投食口就会落下少量的食物。如果一只猪去踩踏板,另一只猪就有机会抢先吃到另一边落下的食物。但当小猪踩踏板时,大猪会在小猪跑到食槽之前刚好吃光所有的食物;大猪踩动了踏板,则有机会在小猪吃完落下的食物之前跑到食槽,争吃到另一半食物。那么,两只猪各会采取什么策略?当然是小猪等在食槽边,而大猪不知疲倦地奔忙于踏板和食槽之间。因为,小猪踩踏板将一无所获,不踩踏板反而能吃上食物。对小猪而言,无论大猪是否踩动踏板,不踩踏板总是好的选择。反观大猪,已明知小猪不会去踩动踏板,自己亲自去踩踏板还有点吃的,总比不踩强,所以只好去踩踏板。
范式博弈:GOO公司和SAM公司存在利益关系,二者的收益会随着博弈的变化而不断更替。如下图:
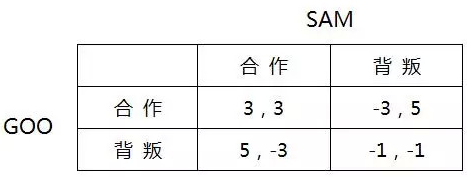
双方各有两个可选策略“合作”与“背叛”,格中的四组数据表示四个博弈结局的各自收益,每组数据的第一个数字表示GOO公司的收益,后一个数字表示SAM公司的收益。现在我们站在GOO公司的角度来思考整个博弈策略。假如SAM选择合作,那么我方合作的收益是3,而我方背叛的收益是5,我方应该选择背叛;假如SAM选择背叛,那么我方合作的收益是 -3,而我方背叛的收益是-1,我方还是应该选择背叛。同理,SAM公司也会做出相同的选择。最后我们发现,本次博弈的双方都采取了背叛策略,各自的收益都为-1,这是一个比较糟糕的结局,尽管对任何一方来说都不是最糟糕的那种。但博弈的次数往往不止一次,当二家公司经历了多次背叛策略的博弈之后,发现公式上还有一个(3,3)收益的双赢局面,这个结果显然要好很多,因此二家公司在之后的博弈过程中必然会尝试互建信任,从而驱使双方都选择合作策略。但假使双方都知道博弈次数是有限的,也许下一次博弈就是最后一次,那么为了避免对方在最后一轮博弈中选择背叛而使我方遭受-3的损失,于是双方都会采取了背叛策略,最后的博弈结果又回到了(-1,-1)。由此可见,随着次数的变化,博弈的性质也会发生变化,纳什均衡点会发生变化。
早期经济学的“理性人假设”及其谬误:“博弈论”诞生【之前】,微观经济学在进行数学建模的时候,通常都会引入一个“理性人假设”——假定市场的行为主体(公司 or 个人)是充分理性滴(此处的“充分理性”还隐含着“掌握充分的信息”)。
为啥一定要引入这个假设捏?是为了数学建模的需要(否则没法建模)。但这个假设其实非常扯蛋——对任何一个国家(哪怕是成熟的民主国家),大多数人都很平庸(他们的共同点之一是非常【不】理性)。充分理性(并且掌握了充分信息)的个人,就算有,那也绝对是凤毛麟角。而“理性人假设”竟然设定市场的行为主体全都是充分理性的。这不是睁着眼睛说瞎话嘛?有了博弈论之后,这个非常扯蛋的“理性人假设”就可以丢到垃圾桶里了 🙂 为了帮大伙儿理解,俺用两种不同的理论来解释同一个现象。
比如说,市场上存活的大部分公司,他们生产的商品都是能满足市场需求滴。
旧的经济学理论(理性人的解释)会说——所有公司的老板都充分理性,也掌握了充分的信息,知道应该生产何种商品,才能满足市场需求。
新的经济学理论(博弈论的解释)会说——公司的老板既有聪明的,也有傻逼的。傻逼公司生产的商品没人要,自然会亏损并倒闭。随着时间的推移,经过【自然选择】,活下来的公司当然是那些聪明的(至少不是太笨的)。
对【经济学理论】的影响:
谈“博弈论”的影响,当然首先要谈它对【经济学】的影响。博弈论的问世堪称“经济学在20世纪最重要的革命”。
有了博弈论,就不再需要那个扯蛋的“理性人假设”了。这是“博弈论”诞生后对微观经济的重大影响。除了这个影响,还有很多其它的影响。比如说:(博弈论诞生前)传统的微观经济学以“供给/需求”来建立【价格】的数学模型。这个模型只考虑了“供应量/需求量”的变化对价格的影响,而完全【不】考虑供给双方的【力量对比】。
【力量对比】是啥意思捏?如果供给双方中,一方变得强势或另一方变得弱势。即使供应量与需求量都维持不变,价格也会发生变动(朝着对强势方有利的方向移动)。
为了帮大伙儿理解上述这句话,拿前段时间好多名人吹嘘的臭名昭著的【996工作制】来现身说法。咱们【没有】真正意义上的工会;各个城市的【官方工会】替谁说话都是大家都懂的,而不是替工人(白领、蓝领)说话。在工会缺位的情况下,资方自然变得更强势,而劳方变得更弱势。【996工作制】就是在这个大背景下发展起来滴。通过变相延长工作时间,也就相当于变相压低了劳动力的价格(请注意,劳动力本身也是一种商品)。
实际情况不仅于此。因为996工作制已经开始普及——今年(2020)深圳开始搞相关的试点,企图把这种工作制【合法化】。当这种工作制逐渐普及之后,会在人力资源市场产生某种【正反馈】,从而导致某种更糟糕的后果(对资方而言则是更美好的后果)。然而作为管理者而言,追求效率才是正确的提升竞争优势的方向。